How to Use Curl and Divergence to Describe Function

X i z 2 e 3 x j x 2 7 z k. Divergence measures the outflowing-ness of a vector field.

Divergence Article Khan Academy

The formula for divergence is.

. The divergence of a curl function is a zero vector. Which leads to the well known Cauchys integral theorem. In this video i have explained Gradient Divergence and Curl of function with following Outlines0.

The Gradient is what you get when you multiply Del by a scalar function Grad f Note that the result of the gradient is a vector field. Here are two functions. The divergence gradient and curl all involve partial derivatives.

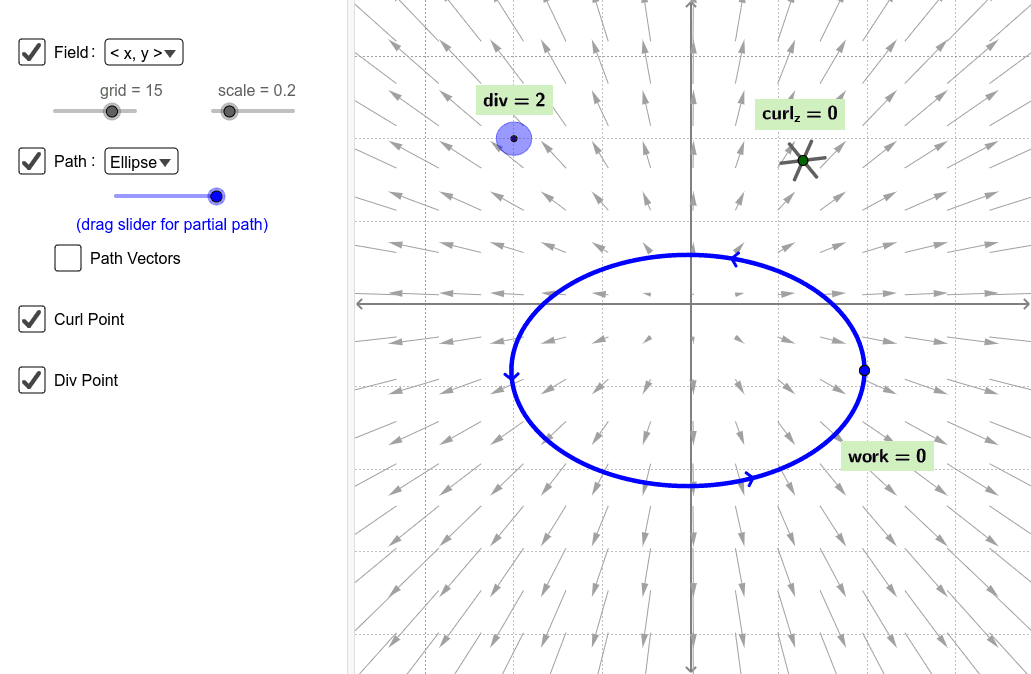
The curl of a gradient function is 0. The curl of F is. The divergence is the limit of the ratio outward flux integral of the field over a sphere sayenclosed volume as a region like a little sphere shrinks to a point.

You position yourselves into a square formation. The length and direction of a curl function does not depend on the choice of coordinates system I. Gradient Divergence and Curl.

In the next few videos Im gonna describe what it is mathematically and how you compute it and all of that but here I just want to give a very visual understanding of what it is that its trying to represent. First we will compute the curl using our cross-product formula replacing P Q and R from our vector field and taking the respective partial derivatives. Assuming the river flows perfectly-evenly youll all float along together.

From an answer here I got Greens theorem for functions in the complex plane. Jacobian vars curl F. The gradient divergence and curl are the result of applying the Del operator to various kinds of functions.

Keep in mind though divergence is used in all sorts of contexts which. As before this mnemonic only works if F displaystyle mathbf F is defined in Cartesian coordinates. Properties of Curl and Divergence Given that F is a scalar function F 0.

The integrals in practice problem 1. I think that fluid flow is the best setting for the painting of an intuitive picture of curl and divergence. Below are good examples of this situation.

The divergence and curl describe what happens to you and your friends as you float down the river together. Vector Sym vars free_symbols F curl F. F 2y cosx i z2e3xj x2 7zk F 2 y cos.

Section 6-1. The Curl of a Vector Field Consider the vector fields Fx yz Px yzˆi Qx yzˆjRx yzkˆ r The curl of F is another vector field defined as. Therefore the divergence at 0 2 1 is e 0 1 4 4.

F i j k x y z f g h h y g z f z h x g x f y. It will also provide a clear insight about the calculation of Divergence and Curl of a. From which I then get.

In many cases it is easier to evaluate the line integral using Greens Theorem than directly. F z d z i f d x d y i 1 f x i f y d x d y. F is a vector and the curl of F is a vector.

Find the curl and divergence of the vector field F x y z e x cos. Worked examples of divergence. Imagine a fluid with velocity field vecv.

Given a single fluid element the curl measures the rotation of infinitesimally neighboring fluid elements about the given fluid element. In terms of the differential operator the curl of F P Q R x y z i j k ˆ ˆ ˆ curl F r A key point. X e x y y z z y z 2 e x z 2 y z.

The divergence of a vector field F f g h is. The curl function is used for representing the characteristics of the rotation in a field. So in a way you can use a toilet bowl to understand all three of these concepts.

The divergence is an operator which takes in the vector-valued function defining this vector field and outputs a scalar-valued function measuring the change in density of the fluid at each point. Weve gotten to one of my all-time favorite multi-variable calculus topics divergence. The divergence of a vector field is a scalar function.

Y e x sin. Alright lets put these two ideas to work with an example. The field giving the velocity of the rivers flow.

Curl F F ˆi ˆj kˆ y P x Q x. Curl and divergence are two operators that play an important role in electricity and magnetism. If v is the velocity field of a fluid then the divergence of v at a point is the outflow of the fluid less the inflow at the point.

Jacobian F pt The nabla del operator. Hence if a vector function is the gradient of a scalar function its curl is the zero vector. - Voiceover Alright everyone.

If F represents the velocity of a fluid then more fluid is flowing out than flowing in at point 0 2 1. Is a vector function of position in 3 dimensions that is then its divergence at any point is defined in Cartesian co-ordinates by We can write this in a simplified notation using a scalar product with the vector differential operator. Where are the component functions of.

Function pt curl ForwardDiff. Suppose you are tubing down a river with three friends. The divergence of F is.

For problems 1 3 compute div F div F and curl F curl F. Here are two simple but useful facts about divergence and curl. F x y z f g h f x g y h z.

F 4y 1 i xy2j x 3yk F. The curl vecnablatimesvecv can be interpreted as follows. To calculate it take the gradient of the function first then take the divergence of the result.

The computation of the Jacobian differs whether the problem is treated numerically or symbolically. The divergence would be where is the water flowing and how much is flowing the gradient would be At this point of the bowl how fast is the water moving or what is the pressure of the water at this point and the curl would be How much is the water twisting in this section of the bowl Gets. Aside from the derivative definition both curl and divergence have integral definitions.

This problem will help to calculate the Gradient of a scalar function. Notice that the divergence of a vector field is a scalar field. The curl of a function is similar to the cross product of two vectors hence why the curl operator is denoted with a.

F z d z f x y f y x i f x x f y y d x d y.

Curl And Divergence Kristakingmath Youtube

Vector Fields Divergence Curl And Line Integrals Geogebra

Calculus Curl And Divergence Mathematics Stack Exchange